Introduction

Happy π Day! The constants we hold dear tell a story of our intellectual history. In a universe of universal flux, constants are really the only thing we can (literally) count on always being there for us when we need them. Or can we?

The constant π is about lengths and circles, and lengths and circles give rise to angles, trigonometry, and so on. π is, therefore, the key to the Gateway of Geometry. Today, 03/14 (in the US way of writing it), is the date that lists the first three digits of π, defined as the ratio of the length of the diameter of any circle to its circumference. That’s right: any circle whatsoever, regardless of how large it is drawn (provided you’ve drawn it on a flat plane and not, say, on a balloon!)

Why is π Constant?

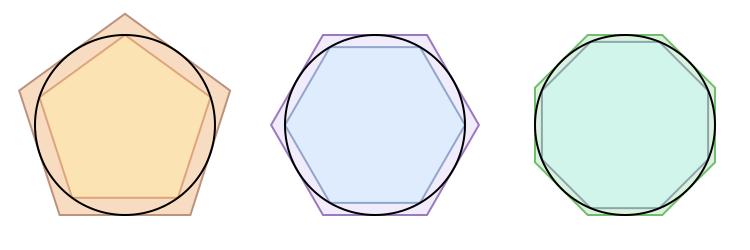
Why is π constant at all? It's a very reasonable question to ask, and one that requires proof to answer. Perhaps the simplest way to do this is to approximate the circumference of a circle by sequences of regular polygons in the plane: one collection whose perimeters form an upper bound and one a lower bound on the circle’s circumference. The polygons are constructed of lines, and having the technology to measure those, one proceeds by the “method of exhaustion” to compute the irrational, transcendental π.

Limits and Constancy

There are plenty of interesting facts about π, and they can be found in abundance, especially today, what I want to focus on is that the “method of exhaustion” is a scientific rather than mathematical technique. The mathematical fact that π is constant at all requires a literal leap of faith: if the process continues this way, and this pattern holds, then we can say what happens at the end. To prove that π is constant, mathematicians had to rigorously define the idea of a limit.

To my knowledge, which is always gratefully expanded upon, there is no mathematically rigorous reason to suspect that π is constant without using the notion of a limit. I do not know of a proof that π is constant that does not use the idea of a limit or a proto-limit. I’m not a math historian, so this curiosity I see might be on the part of ignorance. Is there pre-limit proof that pi is constant that would satisfy a modern mathematical audience?

For now, I’ll let this particular issue rest, for it seems to me that the fact that π is constant relies on circular reasoning!

π in Different Geometries

(I’ll say more about limits and their consequences later, suffice it to say that a number of very interesting constants start to bubble up once you have more control over the infinitesimal domains.)

Back to the celebrant of the day. As we saw above, for a circle drawn on a flat plane, π is constant. This is a fact in flat, Euclidean space. When we try to extend the same idea of the constancy of our favored circular ratio to non-Euclidean geometries like a sphere or a hyperboloid (saddle), we find to our dismay/glee that ‘π’ is no longer constant! Check out this wonderful explanation from Yulia Maximenko: π is Not as Constant as You Think!

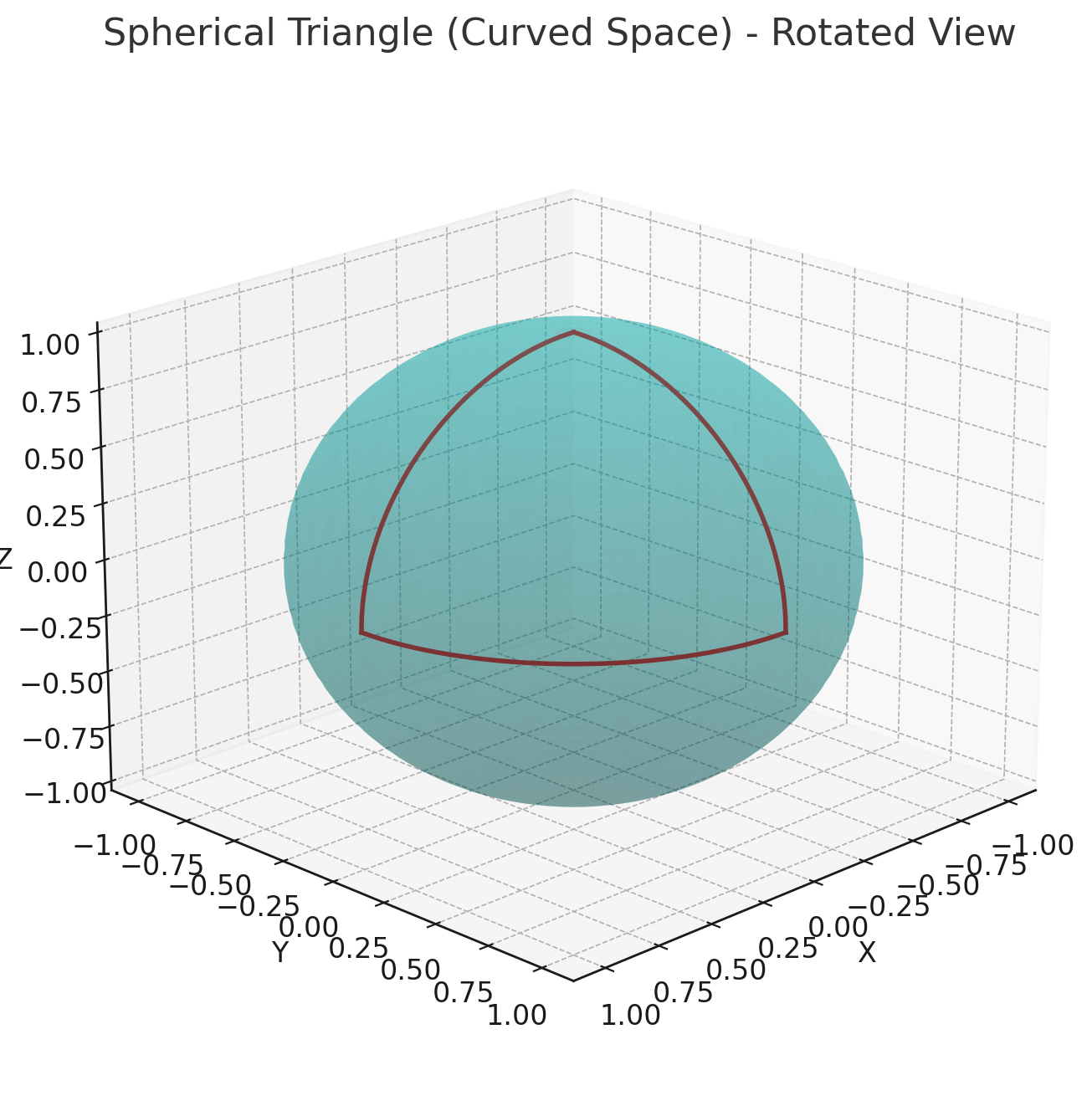
That the constancy of π depends on the flatness of the space a circle is embedded in gives π a two-dimensional flavor, a hint of a higher reality being imposed below. So, is π really constant for us at all here on the surface of the planet? Not so much. But, like many Platonic ideals, it has served us well in the development of our cultures and technologies. We cannot tangibly touch an ideal circle, or count out the value of π, and yet the influence on our physical world is pervasive.