Fibonacci and Pascal's Triangle

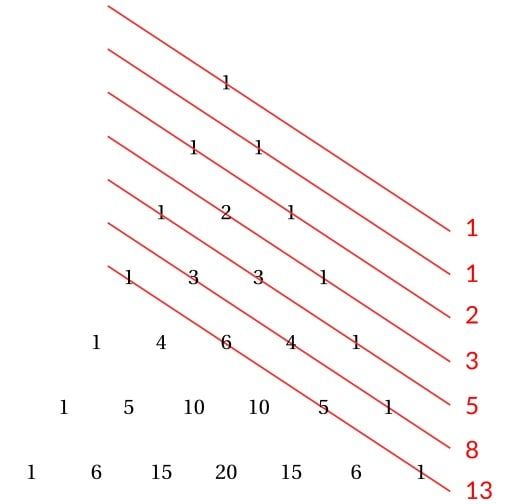
The Fibonacci numbers can be obtained by summing the shallow diagonals of Pascal’s Triangle. But what happens if we add a twist? Consider the polynomials defined by:

\[ P_n(x) = \sum_{k=0}^{\lfloor n/2 \rfloor} \binom{n-k}{k} x^k \]

Where \( \binom{n-k}{k} \) is the binomial coefficient. These polynomials follow:

\[ \begin{aligned} P_0(x) &= 1 \\ P_1(x) &= 1 \\ P_2(x) &= 1 + x \\ P_3(x) &= 1 + 2x \\ P_4(x) &= 1 + 3x + x^2 \\ P_5(x) &= 1 + 4x + 3x^2 \\ P_6(x) &= 1 + 5x + 6x^2 + x^3 \\ P_7(x) &= 1 + 6x + 10x^2 + 4x^3 \end{aligned} \]

Notice that when \( x = 1 \), we recover the Fibonacci numbers: \( P_n(1) = \text{Fibonacci}(n+1) \)!

These polynomials satisfy the recurrence relation:

\[ P_n(x) = P_{n-1}(x) + x P_{n-2}(x) \]

Which resembles a “deformed” Fibonacci recurrence. Examining the ratio of consecutive terms:

\[ Q_n(x) = \frac{P_n(x)}{P_{n-1}(x)} \]

As \( n \to \infty \), \( Q_n(x) \) converges to \( Q(x) \) satisfying:

\[ Q(x) = 1 + \frac{x}{Q(x)} \]

Solving for \( Q(x) \), we find:

\[ Q(x) = \frac{1 + \sqrt{1 + 4x}}{2} \]

For \( x = 1 \), this gives the golden ratio:

\[ Q(1) = \frac{1 + \sqrt{5}}{2} \]