Introduction
The interplay between quantum mechanics, topology, and classical dynamics has inspired many novel approaches in both mathematics and physics. In this work, we propose a geometric framework in which the quantum state space is encoded in the topology of a two-torus. The natural structure of the torus provides a basis for quantum bits: by representing the computational basis states via the fundamental group and first homology, we obtain an inherently topological interpretation of quantum superpositions.
This encoding is enriched by lifting the corresponding cycles (or their linear combinations) to Legendrian submanifolds within a cosphere bundle—a contact manifold that naturally captures both phase and momentum aspects of the system. These Legendrian lifts, endowed with a rich array of contact geometric invariants, serve as a bridge between the abstract quantum encoding and tangible classical dynamics.
Finally, by projecting these Legendrian structures into the punctured cotangent bundle (the classical phase space), we obtain an electromechanical reality wherein the underlying quantum information manifests as observable Hamiltonian dynamics. In what follows, we detail the construction of this framework, discuss its implications for quantum control via electromagnetic potentials, and present a concrete example to illustrate potential applications.
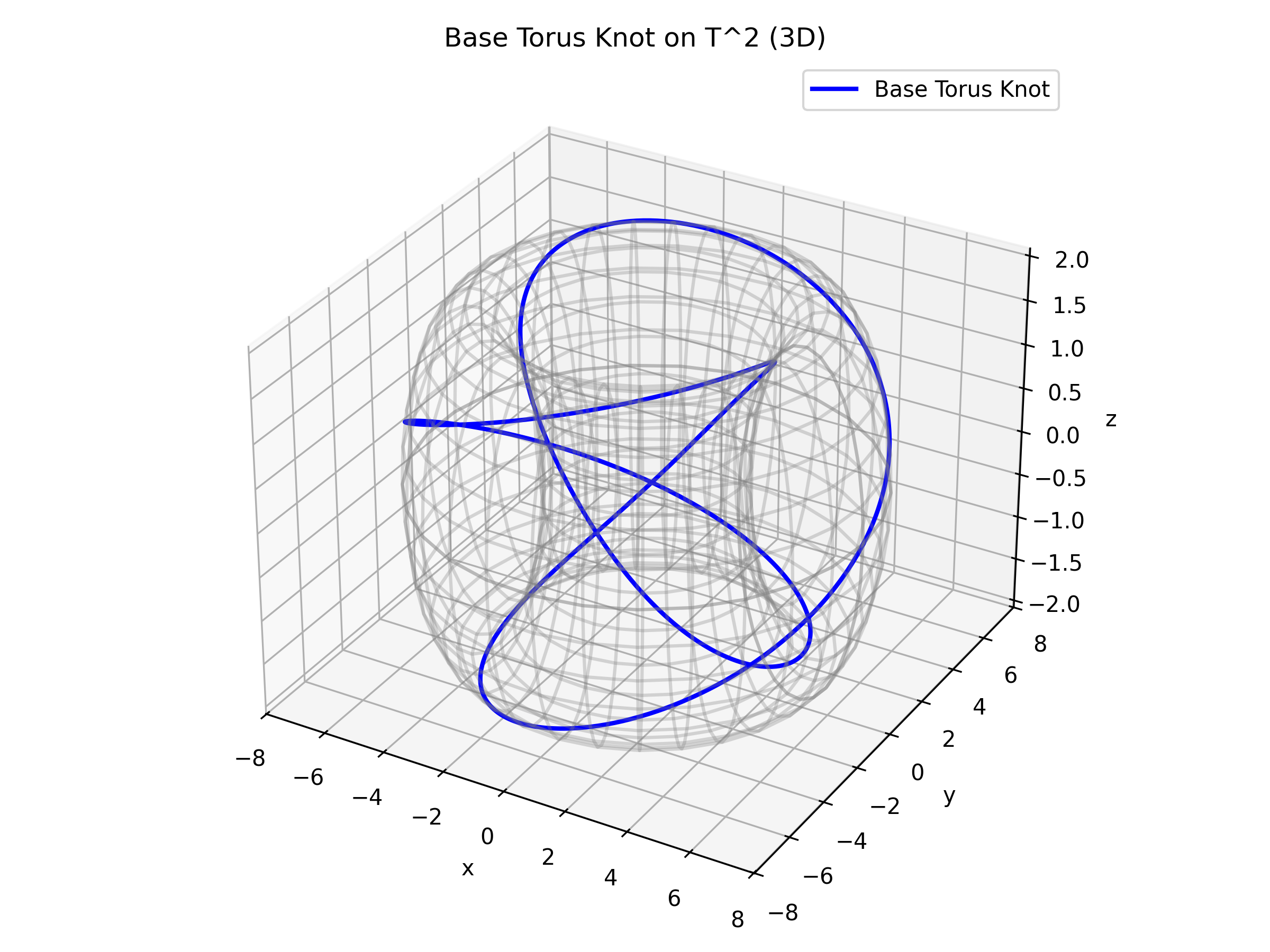
Quantum Encoding on the Torus
The Two-Torus: Geometry and Topology
The two-torus is defined as the Cartesian product of two circles: $$ T^2 \cong S^1 \times S^1. $$ A standard parametrization is given by $$ T^2 = \{ (\theta, \phi) \mid \theta, \phi \in [0,2\pi) \}, $$ with the natural identifications \( \theta \sim \theta + 2\pi \) and \( \phi \sim \phi + 2\pi \). This compact and orientable manifold admits a flat metric inherited from the product of metrics on \( S^1 \).
Fundamental Group and the Quantum Bit
The fundamental group of \( T^2 \) is $$ \pi_1(T^2) \cong \mathbb{Z} \times \mathbb{Z}. $$ Let \( \gamma_0 \) and \( \gamma_1 \) denote the standard generators corresponding to the two independent loops. We identify these loops with the quantum computational basis states: $$ |0\rangle \longleftrightarrow \gamma_0,\qquad |1\rangle \longleftrightarrow \gamma_1. $$ Thus, any quantum state on the torus may be represented as a linear combination $$ |\psi\rangle = \alpha\, |0\rangle + \beta\, |1\rangle, $$ with \( \alpha,\beta \in \mathbb{C} \) (subject to normalization).
Homological Interpretation and Linear Combinations
The first homology group of the torus is $$ H_1(T^2; \mathbb{Z}) \cong \mathbb{Z}^2, $$ generated by the homology classes of \( \gamma_0 \) and \( \gamma_1 \). A general homology class can be expressed as $$ [a] = a_0 [\gamma_0] + a_1 [\gamma_1], \quad a_0,a_1 \in \mathbb{Z}. $$ By extending the coefficients to \( \mathbb{C} \), these classes encode both amplitude and phase: $$ \psi = a_0 [\gamma_0] + a_1 [\gamma_1], \quad a_0,a_1 \in \mathbb{C}. $$ Thus, the qubit structure is naturally embedded in the topological features of \( T^2 \), with qubit operations corresponding to algebraic manipulations in \( H_1(T^2;\mathbb{C}) \).
Visualizing the Encoding
One may visualize the torus as a square with opposite edges identified. In this picture, the two non-contractible cycles (the horizontal and vertical edges) serve as the basis loops. A quantum state is then represented as a weighted superposition of these cycles.
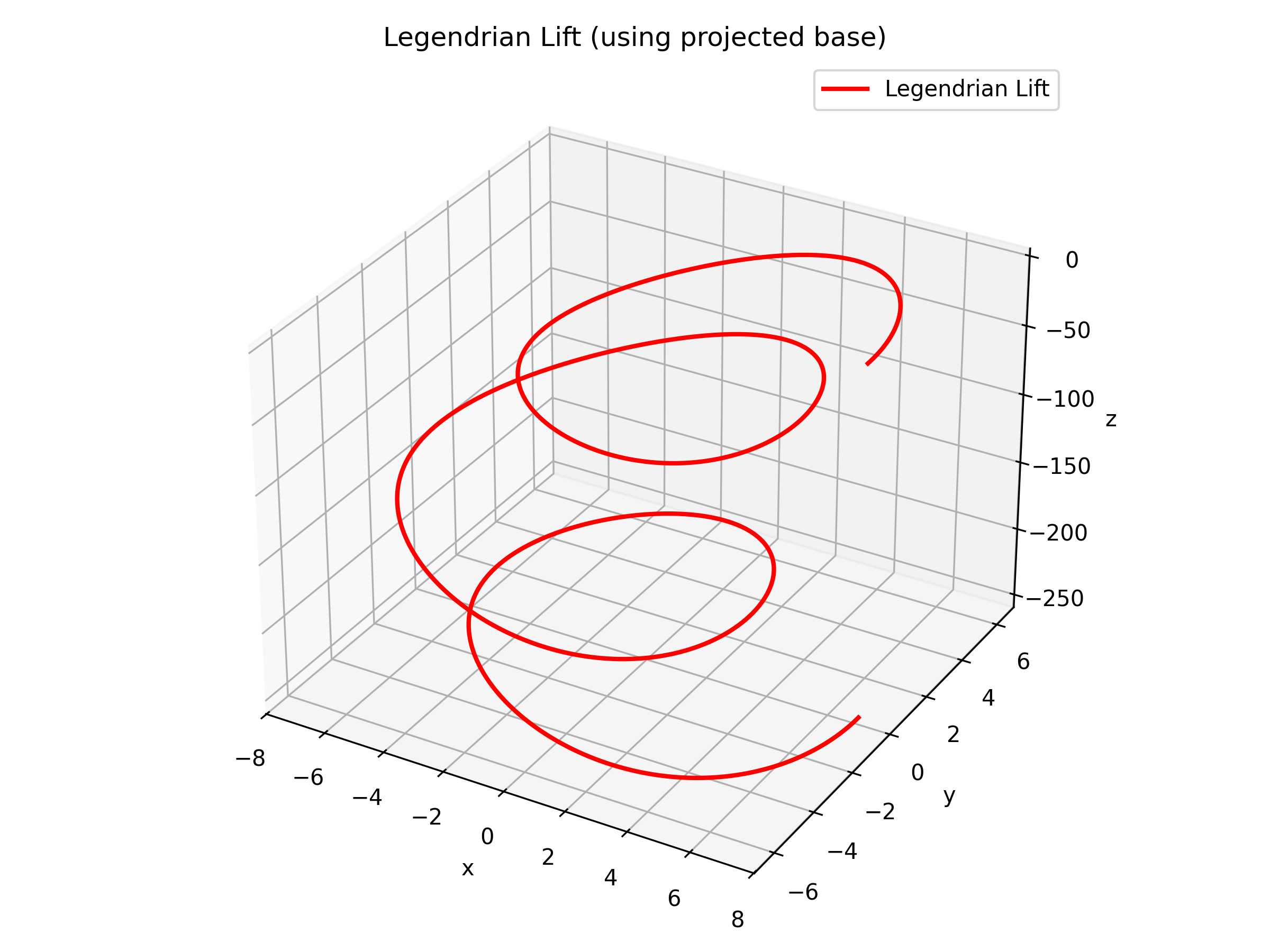
Lifting to Legendrian Submanifolds
The Cosphere Bundle and Contact Geometry
Let \( M \) be a smooth manifold. Its cotangent bundle \( T^*M \) carries a canonical symplectic structure. In local coordinates \( (x^1, \dots, x^n) \) on \( M \) with corresponding momenta \( (p_1, \dots, p_n) \), the Liouville 1-form is defined by $$ \lambda = \sum_{i=1}^n p_i\, dx^i, $$ and the symplectic form is $$ \omega = -d\lambda. $$ The cosphere bundle is defined as $$ S^*M = \{ (x,\xi) \in T^*M : \|\xi\| = 1 \}, $$ where the norm is taken with respect to a chosen Riemannian metric on \( M \). Importantly, the cosphere bundle inherits a natural contact structure.
Legendrian Submanifolds
Within a contact manifold \( (C, \alpha) \), an \( (n-1) \)-dimensional submanifold \( \Lambda \subset C \) is said to be Legendrian if $$ \alpha|_\Lambda = 0. $$ These Legendrian submanifolds serve as the natural analogues of Lagrangian submanifolds in the symplectization of \( C \), capturing both phase and momentum information inherent in the quantum encoding.
Lifting Curves on the Torus to Legendrian Curves
Let \( \gamma: S^1 \to T^2 \) be a smooth closed curve on the torus representing a quantum state (or an element of \( H_1(T^2) \)). We lift \( \gamma \) to a curve \( \tilde{\gamma} \) in the cosphere bundle \( S^*M \) by requiring that $$ \tilde{\gamma}: S^1 \to S^*M, \quad \text{with } \pi \circ \tilde{\gamma} = \gamma, $$ where \( \pi: S^*M \to T^2 \) is the projection. The lift is chosen so that the Legendrian condition $$ \alpha(\tilde{\gamma}'(t)) = 0 \quad \text{for all } t \in S^1, $$ is satisfied.
Interpreting Legendrian Invariants
Legendrian submanifolds come equipped with classical invariants—such as the rotation number and the Thurston–Bennequin invariant—as well as modern invariants derived from Legendrian contact homology. In our framework, these invariants are conjecturally linked to the energies of quantum eigenfunctions via semiclassical quantization conditions.
Schematic Overview
The following diagram summarizes the lifting process:
$$ \gamma \subset T^2 \quad \xrightarrow{\text{Lifting}} \quad \tilde{\gamma} \subset S^*M $$
(Quantum encoding → Legendrian structure)
Projection to the Punctured Cotangent Bundle
Cotangent Bundle as Phase Space
The cotangent bundle \( T^*M \) of a manifold \( M \) is the natural phase space for classical mechanics, endowed with the canonical symplectic form $$ \omega = -d\lambda. $$ To focus on nonzero momentum states, we consider the punctured cotangent bundle $$ T^*M \setminus 0, $$ obtained by removing the zero section.
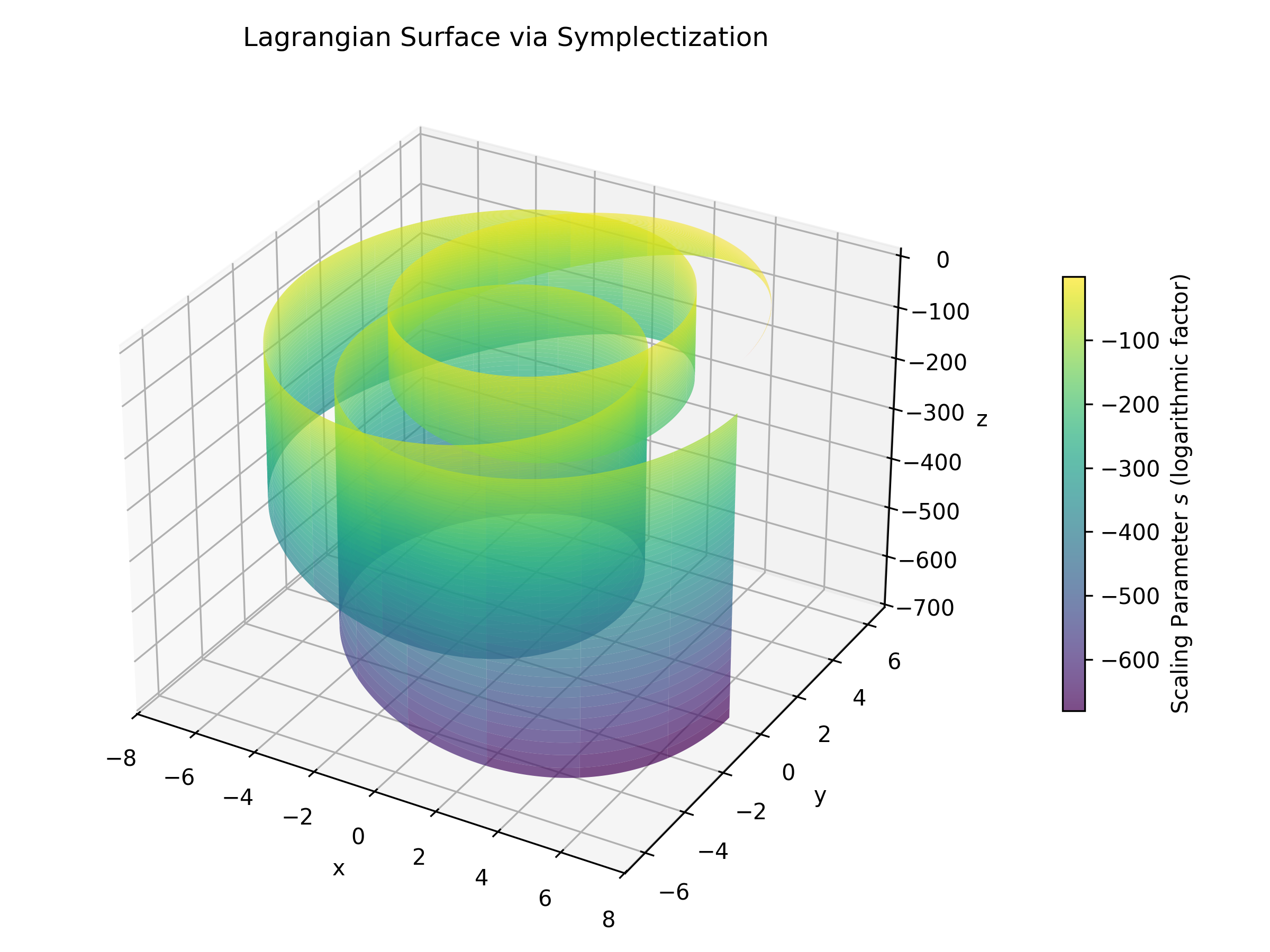
From Cosphere Bundle to Punctured Cotangent Bundle
The cosphere bundle \( S^*M \) is naturally a level set within \( T^*M \). There is a canonical inclusion: $$ i: S^*M \hookrightarrow T^*M \setminus 0. $$ Through this inclusion, Legendrian submanifolds in \( S^*M \) are embedded into the symplectic manifold \( T^*M \setminus 0 \).
Emergence of Electromechanical Dynamics
Once the Legendrian curves are embedded in \( T^*M \setminus 0 \), they can be interpreted as Lagrangian (or pre-Lagrangian) submanifolds that evolve under Hamiltonian flows. This evolution is governed by Hamilton's equations: $$ \dot{x}^i = \frac{\partial H}{\partial p_i}, \quad \dot{p}_i = -\frac{\partial H}{\partial x^i}, $$ where \( H \) is an appropriate Hamiltonian function.
Diagrammatic Summary
Quantum Encoding on T² → Legendrian Submanifolds in S\*(M) → Dynamics in T\*(M)\textbackslash 0
Electromechanical Control of Quantum Dynamics
Phase Identification with Electromagnetic Potentials
Let the coordinates on \( T^2 \) be given by \( (\theta,\phi) \) with $$ \theta \in [0,2\pi), \quad \phi \in [0,2\pi). $$ We identify: $$ \theta \longleftrightarrow \text{phase of the electric potential } A_e, $$ $$ \phi \longleftrightarrow \text{phase of the magnetic potential } A_m. $$ A quantum state expressed as a linear combination of the basis states \( |0\rangle \) and \( |1\rangle \) directly reflects the phase information of the electromagnetic potentials.
Electromechanical Control via External Fields
In practice, external fields can modulate these potentials:
- Electric Control: An external electric field \( \mathbf{E}(t) \) modulates the phase \( \theta \) of \( A_e \), inducing a geometric (Berry) phase in the adiabatic regime.
- Magnetic Control: A time-dependent magnetic field \( \mathbf{B}(t) \) affects the phase \( \phi \) of \( A_m \), with effects analogous to the Aharonov–Bohm phenomenon.
Mathematical Formulation of Dynamics
Suppose the potentials are locally given by $$ A_e = A_e(\theta), \quad A_m = A_m(\phi). $$ Then the overall quantum state is described by the wavefunction $$ \psi(\theta, \phi) = \alpha(\theta)\, |0\rangle + \beta(\phi)\, |1\rangle, $$ where \( \alpha \) and \( \beta \) encode the phase shifts. Under external modulation, the time evolution obeys: $$ i\hbar \frac{\partial \psi}{\partial t} = H(\theta(t), \phi(t))\,\psi. $$
Topological Robustness and Quantum Control
Since the state is represented by a homology class on \( T^2 \), small fluctuations in the potentials yield smooth deformations rather than abrupt changes. This topological protection is reminiscent of the robustness in topological quantum computing.
Example: A Phase-Controlled Two-Level System
Consider a superconducting qubit modeled as a two-level system whose dynamics are governed by external electromagnetic potentials. In many superconducting circuits, such as flux qubits, the energy splitting and tunneling amplitude depend sensitively on the applied magnetic flux and electric drive.
Effective Hamiltonian. A toy model Hamiltonian for the qubit is given by: $$ H = \Delta \cos\!\left(\frac{\phi}{2}\right)\,\sigma_x + \epsilon \cos\!\left(\frac{\theta}{2}\right)\,\sigma_z, $$ where:
- \( \Delta \) represents the tunneling amplitude modulated by the magnetic phase \( \phi \),
- \( \epsilon \) is the energy bias controlled by the electric potential,
- \( \sigma_x \) and \( \sigma_z \) are the Pauli matrices.
Dynamics and Control. With external modulation, the time-dependent Hamiltonian becomes $$ H(t) = \Delta \cos\!\left(\frac{\phi(t)}{2}\right)\,\sigma_x + \epsilon \cos\!\left(\frac{\theta(t)}{2}\right)\,\sigma_z, $$ and the state evolution is governed by $$ i\hbar \frac{\partial \psi(t)}{\partial t} = H(t) \psi(t). $$
Geometric Interpretation. The qubit state, initially represented as a cycle on \( T^2 \), evolves smoothly under modulation. Its lift to the cosphere bundle gives it a Legendrian structure, whose projection onto the cotangent bundle yields the observable electromechanical dynamics.
Speculative Implications. This model suggests that controlling the electromagnetic phases may induce robust, topologically protected evolution of the qubit state—mitigating noise and decoherence.
Perturbations and Nonlinear Dynamics on the Two-Torus
Perturbing the Integrable Setup
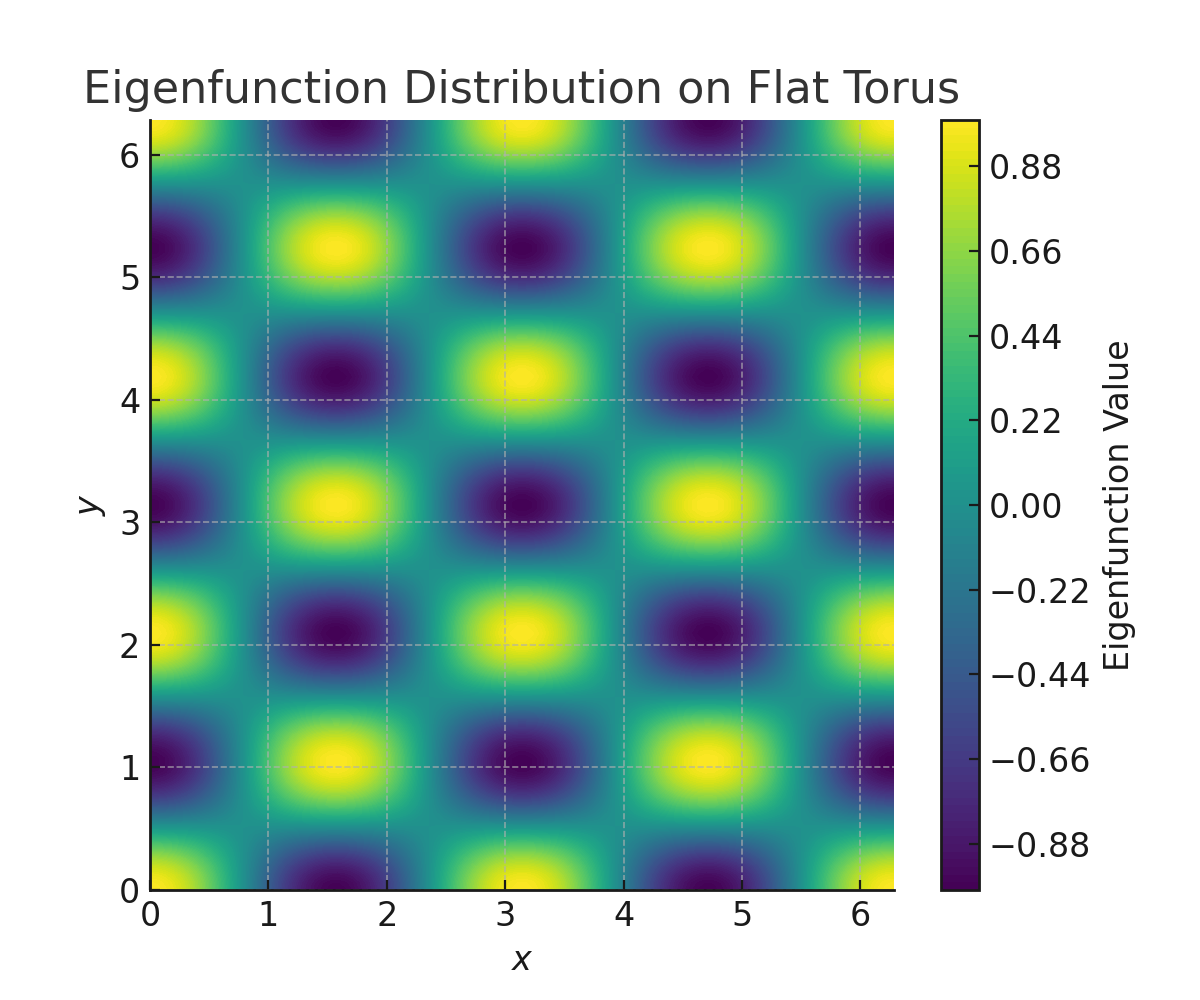
Our starting point is the integrable Hamiltonian on \( T^*T^2 \): $$ H_0(x, p) = \frac{1}{2} \|p\|^2, $$ governing a free particle on the flat torus \( T^2 \). To explore nonlinear effects, we introduce a small perturbation: $$ H_\epsilon(x, p) = H_0(x, p) + \epsilon\, V(x, p), $$ where \( V(x,p) \) is a smooth, periodic potential and \( \epsilon \) is a small parameter.
Analytical Framework and KAM Theory
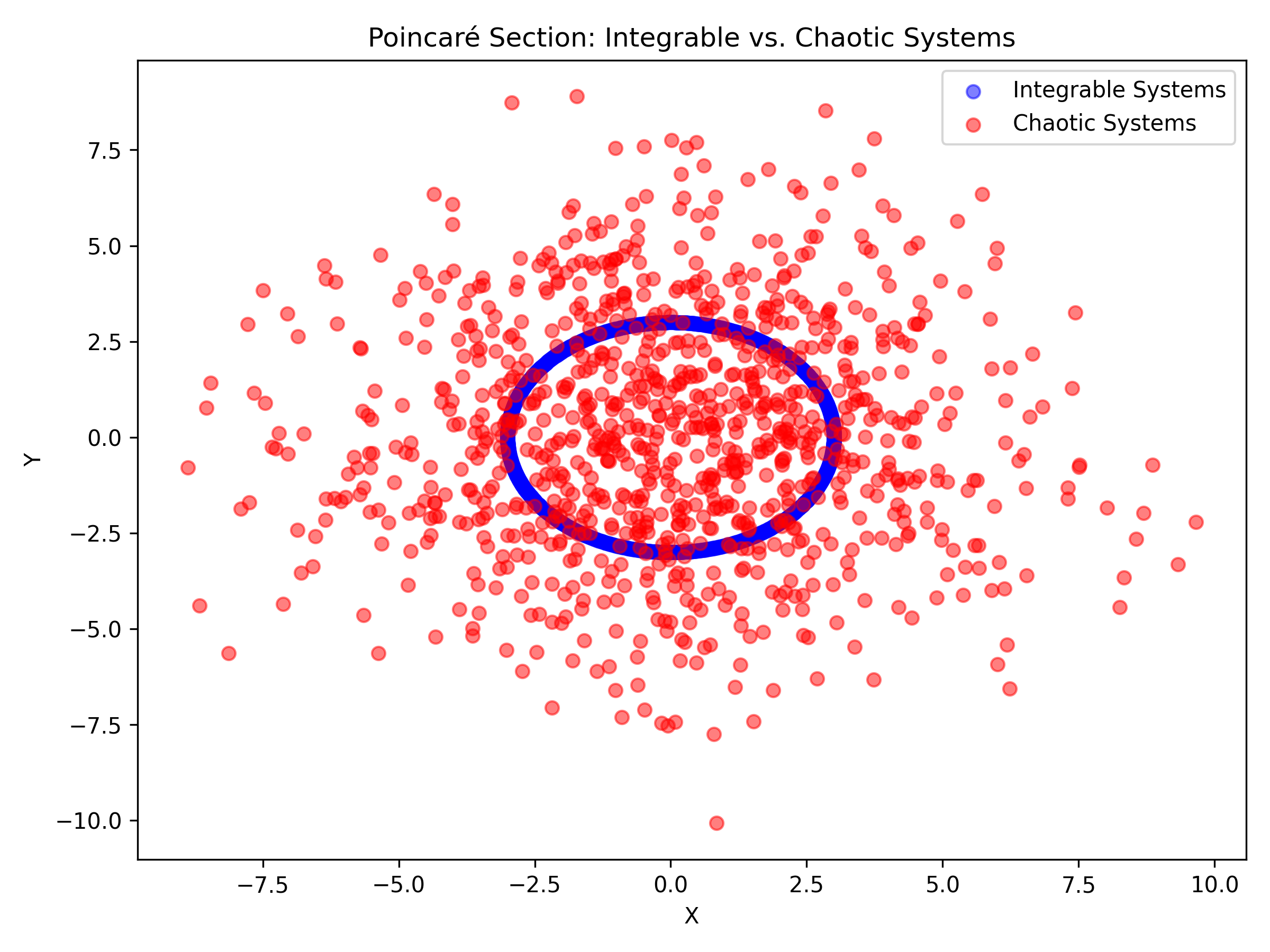
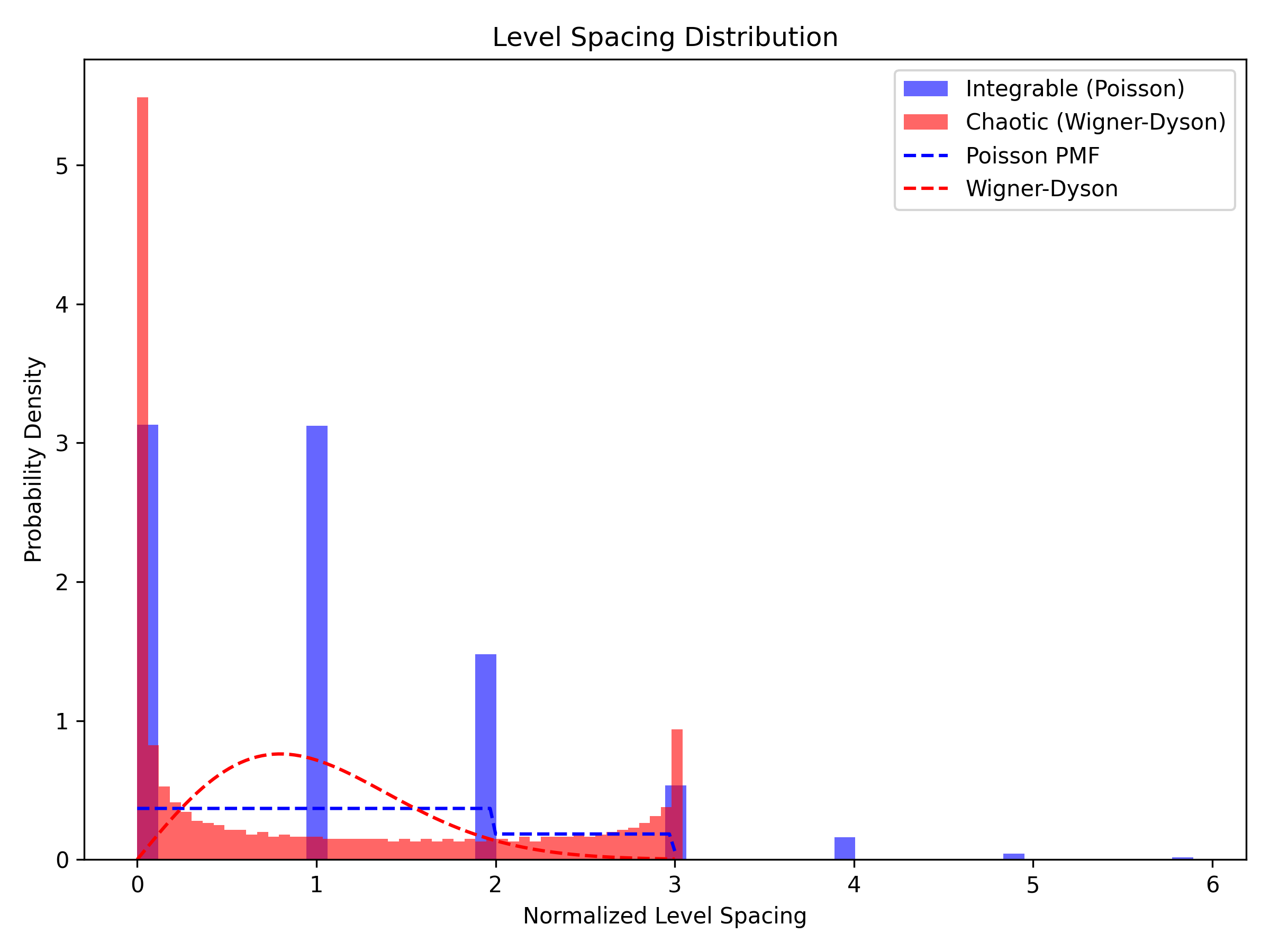
In the perturbed regime, many invariant tori survive in deformed forms as predicted by the KAM theorem. Near resonances, however, these tori may break down, leading to chaotic dynamics. Techniques such as Melnikov methods and normal form analysis provide insight into these phenomena.
Numerical Simulations and Diagnostic Tools
Numerical diagnostics help reveal the richness of the nonlinear behavior:
- Poincaré Sections: Visualize the breakup of invariant tori. (See Figure below)
- Lyapunov Exponents: Quantify sensitivity to initial conditions.
- Spectral Analysis: Compare level spacing distributions (Poisson for integrable, Wigner–Dyson for chaotic systems).
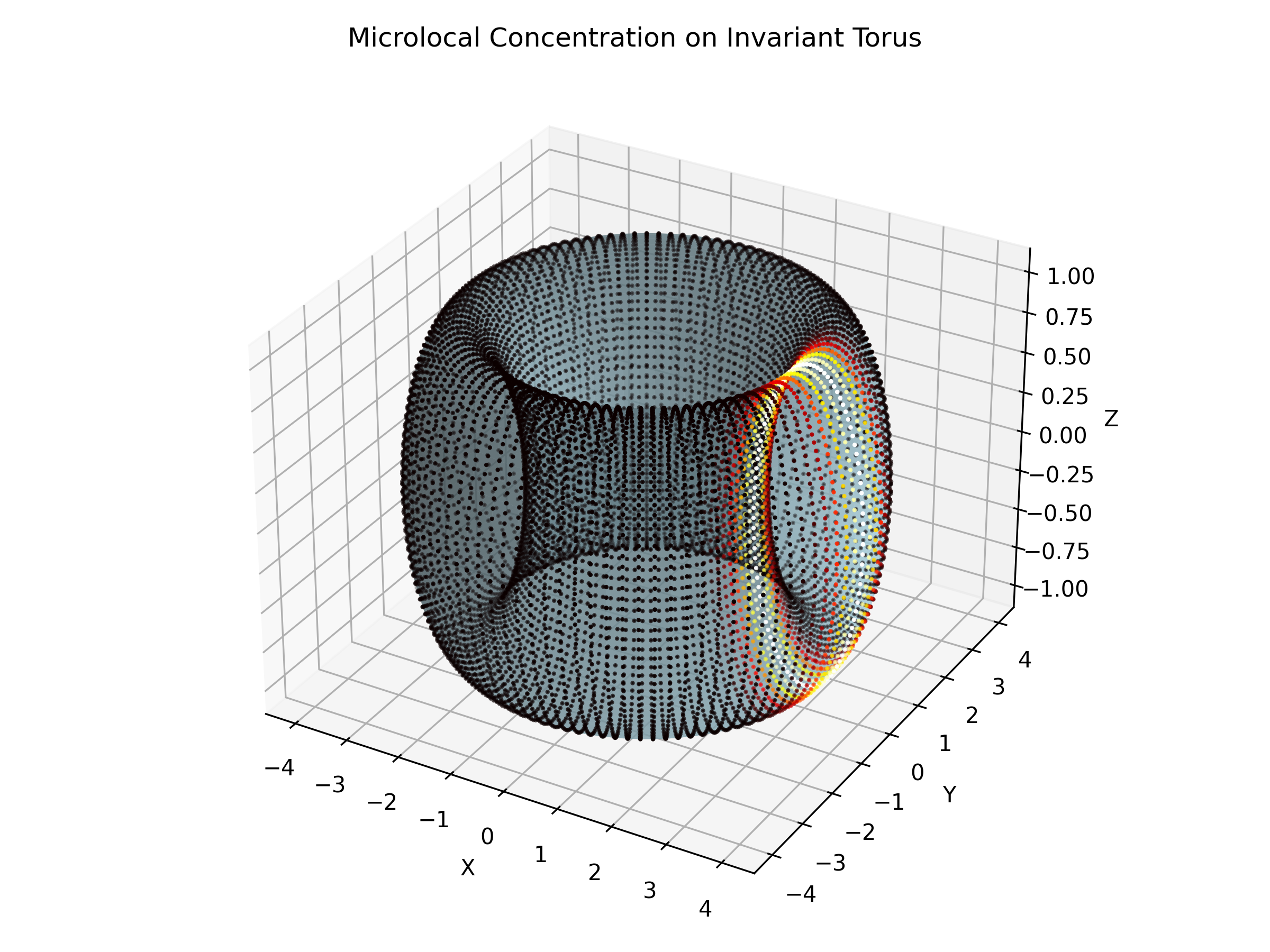
- Microlocal Concentration: Identify scarring phenomena near unstable periodic orbits.
Expected Phenomena
As \( \epsilon \) increases from zero, we expect:
- Persistence of invariant tori in deformed forms for small \( \epsilon \).
- Breakdown of tori near resonances, leading to chaotic layers and resonance islands.
- Quantum signatures such as eigenvalue splitting and scarring near unstable orbits.
- Formation of localized solitonic or vortex structures under nonlinear dynamics.
Outlook and Future Directions
Future work may include refining analytical methods, developing high-resolution simulations, and exploring experimental realizations in superconducting circuits or optical lattices.
Conclusions
In this work we have developed a unified geometric framework that bridges classical and quantum integrability through the interplay of topology, contact geometry, and symplectic techniques. By encoding quantum states on the two-torus \( T^2 \) via its fundamental group and first homology, we have shown how topological structures can serve as a natural basis for quantum bits.
Lifting these topological cycles to Legendrian submanifolds in the cosphere bundle endows the quantum information with additional geometric content—including invariants such as the rotation number and Thurston–Bennequin invariant—that in turn influence the spectral properties of the quantum system.
Furthermore, by projecting the Legendrian submanifolds into the punctured cotangent bundle, we have demonstrated how the same phase-space structure gives rise to observable electromechanical dynamics. This construction naturally leads to a time-dependent, warped-product Lorentzian metric modeling an expanding, and possibly accelerating, spacetime—hinting at connections to early-universe cosmology.
Finally, perturbing the integrable system on \( T^2 \) reveals a rich interplay of nonlinear effects including resonances, chaos, and localized solitonic structures, with potential implications for robust quantum control.
Overall, our work illustrates that the quantum and classical worlds are intimately connected via their underlying geometric and topological structures, opening new avenues for both theoretical exploration and practical applications in quantum information processing and gravitational physics.